17 July 2023
The full article can be found on medium
A common concept in Transportation and Urban Planning is the concept of Accessibility to services and amenities; not to be confused with Universal Accessibility which is more related to inclusive design. Examples of accessibility can be:
These questions often translate to Accessibility or Reach Map analyses that aim to create a single - or a series of - isochrones (lines/areas of equal travel time or distance); similar to contour lines on topo maps (lines of equal elevation). The term isochrone is used interchangeably to refer to both time and distance. An advantage of isochrones is that they transform a routing problem into a spatial join problem. Instead of having to calculate routes between a source and a multitude of destinations (POIs) which can be time-consuming, you can instead intersect the isochrone (polygon/area of equal distance or travel time) with a POI layer represented by points or building polygons (spatial join) and know with good accuracy how far each POI lies from the start point for a given mode of travel.
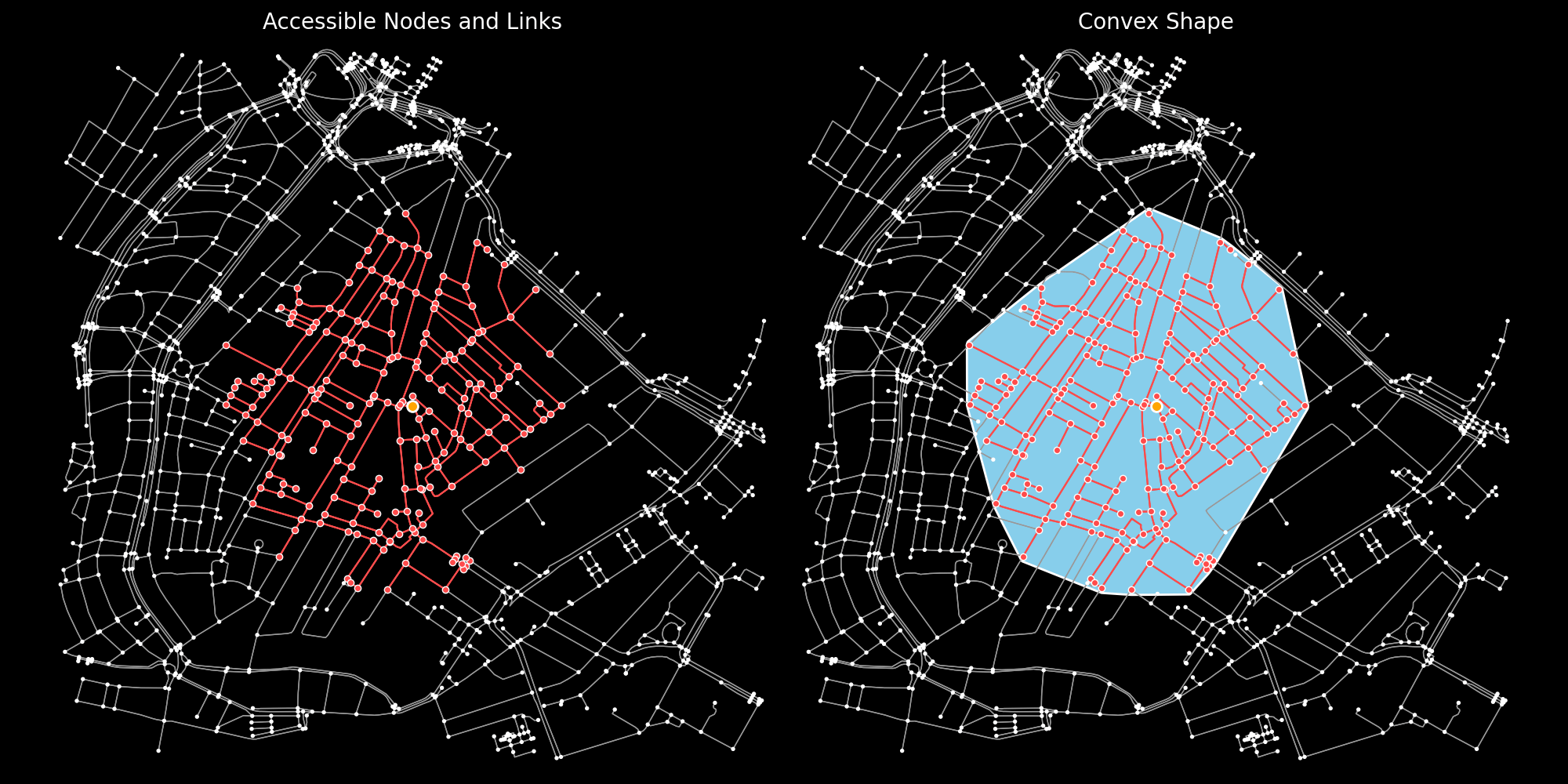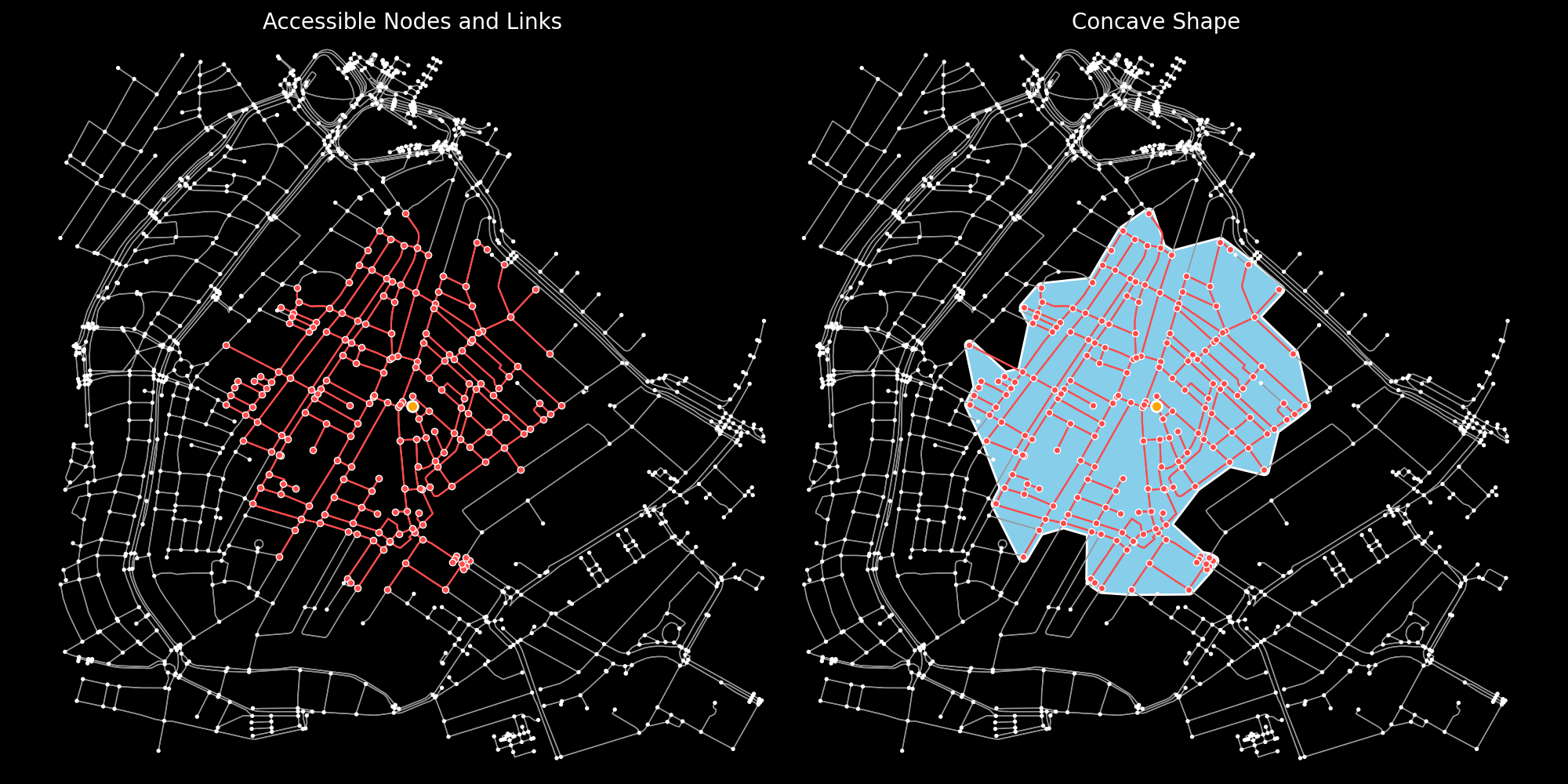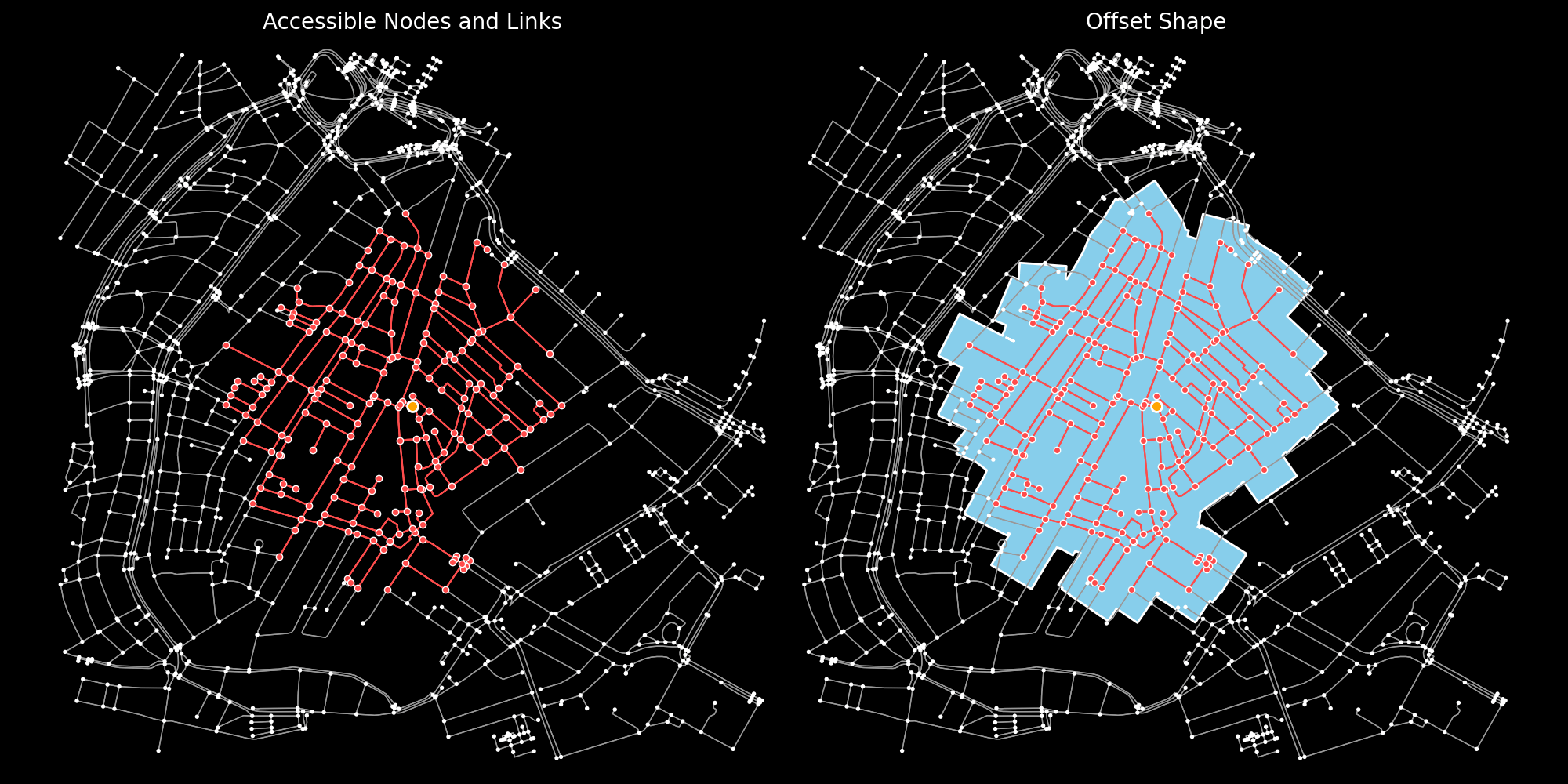
However, An aspect of reach maps that is often overlooked is how the accessibility surface is actually computed or constructed. The final result is a polygon but the underlying calculations to determine the accessible area(s) are graph/network calculations (commonly ego graph or ego network). These calculations yield a subset of nodes (intersections) and links/edges (roads) that are within the required distance or travel time. Transforming nodes and links into a shapeAn additional step is needed to transform or approximate a shape (line or polygon) from those nodes and links. The correct choice of methodology or algorithm to approximate a shape can depend on the:
There are two main groups of methodologies to approximate accessibility polygons: Computational Geometry methods (vector calculations) Spatial/Grid interpolation methods (raster calculations)
The full article can be found on medium